
6
th
Grade Mathematics ● Unpacked Contents
For the new Standard Course of Study that will be effective in all North Carolina schools in the 2018-19 School Year.
This document is designed to help North Carolina educators teach the 6
th
Grade Mathematics Standard Course of Study. NCDPI staff are
continually updating and improving these tools to better serve teachers and districts.
What is the purpose of this document?
The purpose of this document is to increase student achievement by ensuring educators understand the expectations of the new standards. This
document may also be used to facilitate discussion among teachers and curriculum staff and to encourage coherence in the sequence, pacing,
and units of study for grade-level curricula. This document, along with on-going professional development, is one of many resources used to
understand and teach the NC SCOS.
What is in the document?
This document includes a detailed clarification of each standard in the grade level along with a sample of questions or directions that may be used
during the instructional sequence to determine whether students are meeting the learning objective outlined by the standard. These items are
included to support classroom instruction and are not intended to reflect summative assessment items. The examples included may not fully
address the scope of the standard. The document also includes a table of contents of the standards organized by domain with hyperlinks to assist
in navigating the electronic version of this instructional support tool.
How do I send Feedback?
Link for: Feedback for NC’s Math Unpacking Documents
We will use your input to refine our unpacking of the standards. Thank You!
Just want the standards alone?
Link for: NC Mathematics Standards

NC 6
th
Grade Math Unpacking - Revised June 2022
2
North Carolina 6
th
Grade Standards
Standards for Mathematical Practice
Ratio and Proportional
Relationships
The Number System
Expressions &
Equations
Geometry Statistics & Probability
Understand ratio concepts
and use ratio reasoning to
solve problems.
NC.6.RP.1
NC.6.RP.2
NC.6.RP.3
NC.6.RP.4
Apply and extend previous
understandings of
multiplication and division
to divide fractions by
fractions.
NC.6.NS.1
Compute fluently with
multi-digit numbers and
find common factors and
multiples.
NC.6.NS.2
NC.6.NS.3
NC.6.NS.4
Apply and extend previous
understandings of
numbers to the system of
rational numbers.
NC.6.NS.5
NC.6.NS.6
NC.6.NS.7
NC.6.NS.8
NC.6.NS.9
Apply and extend previous
understandings of
arithmetic to algebraic
expressions.
NC.6.EE.1
NC.6.EE.2
NC.6.EE.3
NC.6.EE.4
Reason about and solve
one-variable equations.
NC.6.EE.5
NC.6.EE.6
NC.6.EE.7
Reason about one variable
inequalities.
NC.6.EE.8
Represent and analyze
quantitative relationships
between dependent and
independent variables.
NC.6.EE.9
Solve real-world and
mathematical problems
involving area, surface
area, and volume.
NC.6.G.1
NC.6.G.2
NC.6.G.3
NC.6.G.4
Develop understanding of
statistical variability.
NC.6.SP.1
NC.6.SP.2
NC.6.SP.3
Summarize and describe
distributions.
NC.6.SP.4
NC.6.SP.5

NC 6
th
Grade Math Unpacking - Revised June 2022
3
Standards for Mathematical Practice
Practice
Explanation and Example
1. Make sense of
problems and
persevere in solving
them.
In grade 6, students solve real world problems through the application of algebraic and geometric concepts. These problems
involve ratio, rate, area, and statistics. Students seek the meaning of a problem and look for efficient ways to represent and solve
it. They may check their thinking by asking themselves, “What is the most efficient way to solve the problem?”, “Does this make
sense?”, and “Can I solve the problem in a different way?”. Students can explain the relationships between equations, verbal
descriptions, tables and graphs. Mathematically proficient students check answers to problems using a different method.
2. Reason abstractly
and quantitatively.
In grade 6, students represent a wide variety of real-world contexts using numbers and variables in mathematical expressions,
equations, and inequalities. Students contextualize to understand the meaning of the number or variable as related to the problem
and decontextualize to manipulate symbolic representations by applying properties of operations.
3. Construct viable
arguments and
critique the reasoning
of others.
In grade 6, students construct arguments using verbal or written explanations accompanied by expressions, equations,
inequalities, models, and graphs, tables, and other data displays (i.e., box plots, dot plots, histograms, etc.). They further refine
their mathematical communication skills through mathematical discussions in which they critically evaluate their own thinking and
the thinking of other students. They pose questions like “How did you get that?”, “Why is that true?” “Does that always work?” They
explain their thinking to others and respond to others’ thinking.
4. Model with
mathematics.
In grade 6, students model problem situations symbolically, graphically, tabularly, and contextually. Students form expressions,
equations, or inequalities from real world contexts and connect symbolic and graphical representations. Students begin to explore
covariance and represent two quantities simultaneously. Students use number lines to compare numbers and represent
inequalities. They use measures of center and descriptions of variability of data displays (i.e., box plots and histograms) to
summarize and describe data. Students need many opportunities to connect and explain the connections between the different
representations. They should be able to use all of these representations as appropriate to a problem context.
5. Use appropriate tools
strategically.
Students consider available tools (including estimation and technology) when solving a mathematical problem and decide when
certain tools might be helpful. For instance, students in grade 6 may decide to represent figures on the coordinate plane to
calculate area. Number lines are used to understand division and to create dot plots, histograms, and box plots to visually
compare the center and variability of the data. Additionally, students might use physical objects or applets to construct nets and
calculate the surface area of three-dimensional figures.
6. Attend to precision.
In grade 6, students continue to refine their mathematical communication skills by using clear and precise language in their
discussions with others and in their own reasoning. Students use appropriate terminology when referring to rates, ratios, geometric
figures, data displays, and components of expressions, equations, or inequalities.
7. Look for and make
use of structure.
Students routinely seek patterns or structures to model and solve problems. For instance, students recognize patterns that exist in
ratio tables recognizing both the additive and multiplicative properties. Students apply properties to generate equivalent
expressions (i.e., 6 + 2 = 2 (3 + ) by distributive property) and solve equations (i.e. 2+ 3 = 15, 2 = 12 by subtraction property
of equality, = 6 by division property of equality). Students compose and decompose two- and three-dimensional figures to solve
real world problems involving area and volume.
8. Look for and express
regularity in repeated
reasoning.
In grade 6, students use repeated reasoning to understand algorithms and make generalizations about patterns. During multiple
opportunities to solve and model problems, they may notice that / ÷ / = / and construct other examples and models
that confirm their generalization. Students connect place value and their prior work with operations to understand algorithms to
fluently divide multi-digit numbers and perform all operations with multi-digit decimals. Students informally begin to make
connections between covariance, rates, and representations showing the relationships between quantities.
Return to: Standards

NC 6
th
Grade Math Unpacking - Revised June 2022
4
Ratio and Proportional Reasoning
Understand ratio concepts and use ratio reasoning to solve problems.
NC.6.RP.1 Understand the concept of a ratio and use ratio language to:
● Describe a ratio as a multiplicative relationship between two quantities.
● Model a ratio relationship using a variety of representations.
Clarification
Checking for Understanding
This standard addresses the definition and nature of ratios.
A ratio is a comparison of two or more related quantities.
For example: “The ratio of wings to beaks in the bird house at the zoo was 2:1,
because for every 2 wings there was 1 beak.”
“For every vote candidate A received, candidate C received nearly three votes.”
These quantities may:
● be discrete, e.g., 5 cats (can’t have ½ a cat!)
● be continuous, e.g., 3.5 ft. (can be divided into smaller parts.)
● have the same or different units.
Students should be exposed to all combinations of these quantity types.
Using the concept of a ratio, students write ratios from known quantities in a variety
of ways, including writing ratios using an initially unknown quantity. For example, in
the ratio of 12 boys to 13 girls in a class, it is possible to describe this situation with a
ratio of 12 boys to 25 students even though the total number of students was not
directly given in the situation.
Describing the multiplicative relationships of ratios.
In elementary school students relied largely on additive reasoning to solve problems.
While additive reasoning can be used when solving ratio problems, 6
th
grade
students will transition to multiplicative reasoning to solve ratio problems.
Students will describe two multiplicative relationships in ratios:
1. The multiplicative relationship within a ratio. Students will use the term
rate to describe these relationships. In ratios, the rate is the multiplicative
change from one quantity to the other quantity.
2. The multiplicative relationship between two ratios. Students will use the
term scale factor to describe these relationships. In ratios, the scale factor
shows the relative multiplicative change in the magnitude of the quantities
from one ratio to another.
For example: In a simple salad dressing, a certain amount of olive oil is mixed
with vinegar, as seen in the chart below. Describe the multiplicative relationships
seen in the ratios.
Looking from vinegar to olive oil, this relationship has a rate of 3. Looking from olive oil to
vinegar, this relationship has a rate of
1
3
.
Students recorded the number of fish in an aquarium. They used a filled
in circle for guppies and an open circle for goldfish. Below is their
recorded count.
a) What is the ratio of guppies to
goldfish?
b) What is the ratio of guppies to all fish?
c) A student said that they could write the ratio of goldfish to
guppies as 3 to 2. Is this student correct? Demonstrate how you
know using the picture.
Ben is working on puzzles. He noticed
that he completes puzzles at a steady
pace. He recorded, in the table, the
number of puzzles he solved and how many hours it took him.
a) Write as many ratios from the table as you can and identify
which ratios have the same multiplicative relationships.
b) How can these multiplicative relationships be seen in the table?
Using a context, write three ratios that have a rate of 5.
a) What other rate can be found in these ratios?
b) What are the scale factors between your ratios?

NC 6
th
Grade Math Unpacking - Revised June 2022
5
Looking from the first ratio to the second ratio, this relationship has a scale factor of 4.
Looking from the second ratio to the first ratio, this relationship has a scale factor of 1/4.
Note: While the relationship from the second ratio to the first may seem easier to describe
with division, the focus remains on the multiplicative relationship and that by scaling by a
number less than 1 makes the quantities smaller.
Different Representations for Ratios
Ratios can be expressed in many forms, including but not limited to:
● Verbal expressions
● Using a colon
● Ratio boxes and tables
● Fraction notation*
● Double number line
● Coordinate plane
*Fraction notation should be used with caution as fractions represent only part to
whole relationships while ratios can represent both part to part and part to whole
relationships. The overuse of fraction notation may lead students to believing that
ratios are fraction.
A recipe calls for 2 cups of tomato sauce and 3
tablespoons of oil. We can say that the ratio of cups of
tomato sauce to tablespoons of oil in the recipe is 2:3, or
we can say the ratio of tablespoons of oil to cups of
tomato sauce is 3:2.
For each of the following situations, draw a picture and name two ratios
that represent the situation.
a) To make papier-mâché paste, mix 2 parts of water with 1 part of
flour.
b) A farm is selling 3 pounds of peaches for $5.
c) A person walks 6 miles in 2 hours.
Taken from Illustrative Mathematics: Representing a Context with a Ratio
Understand ratio concepts and use ratio reasoning to solve problems.
NC.6.RP.2 Understand that ratios can be expressed as equivalent unit ratios by finding and interpreting both unit ratios in context.
Clarification
Checking for Understanding
This standard asks for students to understand that unit ratios are any ratio in
which one of the quantities being compared in the ratio has the value of 1. For
ratios that compare two quantities, two distinct unit ratios are possible to find,
unless the ratio is 1:1.
For example: In the ratio of 40 dollars for 10 hours of work, the unit ratios
are 1 dollar for 1/4 hour of work and 4 dollars for 1 hour of work.
It is important for students to understand that:
● Unit ratios are equivalent to the original ratio.
● Finding the unit ratios reveals the two rates.
These understandings allow students to interpret the unit ratio in context.
On a bicycle Jack can travel 20 miles in 4 hours.
What are the unit ratios in this situation?
Find the unit ratios for 4 candy bars for 3 dollars.
There are 240 students in the 6
th
grade with 12 teachers.
a) What are the unit ratios?
b) Explain the meaning of each unit ratio.
Return to: Standards

NC 6
th
Grade Math Unpacking - Revised June 2022
6
Understand ratio concepts and use ratio reasoning to solve problems.
NC.6.RP.3 Use ratio reasoning with equivalent whole-number ratios to solve real-world and mathematical problems by:
● Creating and using a table to compare ratios.
● Finding missing values in the tables.
● Using a unit ratio.
● Converting and manipulating measurements using given ratios.
● Plotting the pairs of values on the coordinate plane.
Clarification
Checking for Understanding
Students use ratio reasoning to solve problems. Ratio reasoning includes using
either of the multiplicative relationships (rate or scale factor) in ratios to think
through problems.
For this standard, all initial values should be whole numbers. Numbers formed
in the process of working with the ratios and answers to problems may be
fractions or decimals. (An exception to starting with whole numbers may occur
in some measurement conversions, such as 1 inch to 2.5 cm.)
Students recognize and explain ratio equivalency in multiple ways and with
various representations. Students use a variety of models to assist with solving
problems. Tables, tape diagrams, double number lines, and the coordinate
plane offer ways to approach equivalent ratios. The use of cross-products is not
an expectation of this grade level.
Using Ratio Tables and Unit Ratios
Tables are a natural way to organize and study equivalent ratios. Students work
with vertical and horizontal tables.
Students create ratio tables from a context and then use the multiplicative, and
sometimes additive relationships, to find missing values in a table to solve
problems. A key understanding, students recognize that in a table of equivalent
ratios, the rates of each ratio are also equivalent.
As problems become more complex, students may use the appropriate unit
ratio to find the solution.
Comparing Ratios
There are multiple ways of comparing ratios. In 6
th
grade, students are
expected to use ratio tables to compare the characteristics of the ratios. This
can be accomplished by using multiplicative or additive reasoning to make one
of the quantities in the ratios the same or using a unit ratio to draw a conclusion
based on the values of the other quantity.
Converting and Manipulating Measurements
Students know the conversions facts for:
● Distance in the customary system (inches, feet, yards, and miles)
● The metric system units and the prefixes: milli, centi, deci, deca, hecto,
kilo
● Time
Billy needs to make some lemonade for a bake sale at school. He found two
recipes.
• The first recipe calls for 5 lemons for every 2 quarts of water.
• The second recipe calls for 2 lemons for every quart of water.
Billy prefers a stronger lemon taste in his lemonade.
a) Which recipe should Billy use?
b) Show how you know this in multiple ways.
StoriesTold.com sells its audio books at the same rate and are currently
advertising 3 audio books for $39.
What would 7 audio books cost?
How many audio books could be purchased with $54?
In trail mix, the ratio of cups of peanuts to cups of chocolate candies is 3 to 2.
How many cups of chocolate candies would be needed for 9 cups of
peanuts? How much trail mix would be created using this ratio?
James is making orange juice from concentrated frozen orange juice that he
must mix with water. The concentrated juice is in 12 fluid ounce cartons. The
ratio of orange juice concentrate to water is 12 fluid ounces to 36 fluid
ounces. If James needs 4.5 gallons of orange juice, which is 576 fluid
ounces, how many cartons of concentrated orange juice does he need?

NC 6
th
Grade Math Unpacking - Revised June 2022
7
All other conversion facts, including those between the customary and metric
systems, will be provided.
Students are not expected to use dimensional analysis for conversions or make
multiple unit conversions of different quantities in the ratio. For example,
students will not be asked to convert feet per second to miles per hour.
The Coordinate Plane
Students represent equivalent ratios on a coordinate plane and use the patterns
to solve problems.
Students understand that:
-The origin, (0,0), is an equivalent ratio to all other ratios.
-The coordinates of equivalent ratios form a straight line that is unique to that
set of ratios.
-The points that fall between the coordinates that are on the straight line also
represent equivalent ratios. However, it is only appropriate to draw a line
through the found coordinate(s) if both quantities are continuous.
H ow m a ny centim eters are in 7 feet, given that 1 in. ≈ 2 .5 cm ?
Rima and Eric have earned a total of 135 tokens to buy items at the school
store. The ratio of the number of tokens that Rima has to the number of
tokens that Eric has is 8 to 7. How many tokens does Rima have?
NAEP – Released Item (2013) Question ID: 2013-8M3 #5 M150201
Jacqueline is earning money by babysitting.
She graphed how many hours she worked and
how much money she made for her last two
jobs, one on a weeknight and one on a
weekend.
a) Using the information from the graph,
create a table that shows how much money
she earned for each hour listed on the
graph.
b) Plot the missing points on the graph.
c) What patterns do you see on the graph?
Return to: Standards

NC 6
th
Grade Math Unpacking - Revised June 2022
8
Understand ratio concepts and use ratio reasoning to solve problems.
NC.6.RP.4 Use ratio reasoning to solve real-world and mathematical problems with percents by:
● Understanding and finding a percent of a quantity as a ratio per 100.
● Using equivalent ratios, such as benchmark percents (50%, 25%, 10%, 5%, 1%), to determine a part of any given quantity.
● Finding the whole, given a part and the percent.
Clarification
Checking for Understanding
In this standard, students will be introduced to percents and use percents to
solve basic percent problems.
Ratio Reasoning
One of the essential understandings needed for this standard, is that a percent
is a part to total ratio. The expectation of this standard is that the concepts and
skills learned in the ratio standards will be applied to percents. For this reason,
rules and formulaic approaches should be avoided.
As with ratios, the initial values in percent problems should only be whole
numbers. The answer, or numbers produced finding the answer, may be a
fraction or decimal.
Using ratio reasoning, students should:
● Identify and explain the value of the total in the part to total ratio, as the
total may not be explicitly given.
● Understand that percents cannot be directly compared to other
percents unless the percents are from the same context (have the
same amount associated with 100%). For example, in some cases 20%
of something can be a greater amount than 50% of something.
Benchmark Percents
The benchmark percents should be conceptually developed and their use
encouraged. These percents can be developed using 100s grids and percent
bars. Answering questions with benchmark percents often require the use of
both multiplicative and additive reasoning.
Percents in 6
th
grade
Students will not be asked to work with percents greater than 100 in 6
th
grade.
As with all other standards, this standard may be combined with other
standards to form more steps. For example, a question may be asked for the
students to find the cost of a dinner, given a bill total and a percent being left for
a tip. Finding the tip would be covered under this standard while the cost of the
dinner, the bill plus the tip, would be covered under 6.NS.3, fluently operating
with decimals.
Most dogs fail to become service dogs. In a recent training class, only 7 of the
15 dogs were certified as service dogs. What percent of dogs became
certified service dogs
?
What is 40% of 30?
Kendall bought a vase that was priced at $450. In addition, she had to pay
3% sales tax. How much did she pay for the vase?
Taken from Illustrative Mathematics: Kendall’s Vase – Tax
If 44% of the students in Mrs. Rutherford’s class like chocolate ice cream,
then how many students are in Mrs. Rutherford’s class if 11 like chocolate ice
cream?
A soccer player scored 12 goals during this season. This player scored on
30% of the shots attempted. How many shots were attempted?
Return to: Standards

NC 6
th
Grade Math Unpacking - Revised June 2022
9
The Number System
Apply and extend previous understandings of multiplication and division to divide fractions by fractions.
NC.6.NS.1 Use visual models and common denominators to:
● Interpret and compute quotients of fractions.
● Solve real-world and mathematical problems involving division of fractions.
Clarification
Checking for Understanding
In 5
th
grade, students divided a whole number by a unit fraction or a unit fraction
by a whole number. Students accomplished this division through the use of
physical and visual models. In 6
th
grade, students will continue to use models to
divide fractions.
It is the expectation of this standard that as students use models to solve
division problems involving two fractions, students understand that in order to
find the answer, it is necessary to find a common unit. Through repetition and
reasoning with the models, students develop an algorithm of using common
denominators when dividing fractions. Multiplying by the reciprocal is not the
expectation of this standard and is not supported with understanding at this
grade level.
For example: You are stuck in a big traffic jam on the freeway 1
1
2
miles
away from your exit. You are timing your progress and find that you travel
2
3
of a mile in one hour. If you keep moving at this slow rate, how long will it
be until you get to your exit?
Solution using a physical model (number cubes): Find
how many
2
3
are in 1
1
2
.
Using blocks, we can represent
2
3
and 1
1
2
.
2
3
: Using 3 orange blocks to represent 1 mile, 2 blocks
represent
2
3
mile.
1
1
2
: Using 2 yellow blocks to represent 1 mile, 3 blocks
would represent 1
1
2
miles.
Notice that each color block represents a different value. Each orange block
represents
1
3
and each yellow block represents
1
2
. In order to see how to find how
many
2
3
are in 1
1
2
, we must find a common unit or a common way to represent these
numbers so that we can count.
A common unit of 2 and 3 is 6. This means that we can rework the blocks so that 1
mile is represented by 6
blocks.
This means that 1
1
2
miles are
represented with 9 blocks and
the
2
3
mile covered in 1 hour
can be represented with 4
blocks.
Now with the problems represented, focus back to the question being asked.
A worker is using a polyurethane spray can to seal and protect several new
dinner tables. It takes
2
5
of a can to seal and protect each table. The worker
has 3 full cans of spray. How many tables can the worker seal and protect?
Evaluate the following expressions using models and common denominators.
a)
5
6
÷
1
4
b)
1
2
÷
3
5
c) 15
1
2
÷
3
4
d) 4
2
7
÷ 1
2
3
Susan has
2
3
of an hour left to make cards. It takes her about
1
6
of an hour to
make each card. About how many can she make?
A rectangular parking lot has an area of
2
3
of a square kilometer. The width is
1
2
of a kilometer. What is the quotient of
2
3
and
1
2
and what does it tell us?

NC 6
th
Grade Math Unpacking - Revised June 2022
10
How many
2
3
are in 1
1
2
miles?
Since the
2
3
are represented with 4 blocks, we can repeat the 4 blocks until we cover
the 9 blocks representing the 1
1
2
miles.
This happens 2
1
4
times, representing 2
1
4
hours.
As seen in the problem above, the key understanding of this standard, is that
division problems require common units. This leads the students to the concept
of using a common denominator to divide fractions.
3
2
÷
2
3
→
9
6
÷
4
6
→
9 ÷ 4
6 ÷ 6
=
9
4
1
=
9
4
When finding common denominators, NC.6.NS.4 has a limitation in which
neither denominator should be greater than 12.
As these problems involve fractions, the remainder should be represented as a
fraction. Students are expected to explain the meaning of the quotient in terms
of its context and its relation to the divisor and dividend.
For example: Given that 3 ÷
2
3
= 4
1
2
, what does the 4
1
2
represent?
Solution: The quotient, 4
1
2
, represents 4 groups of
2
3
and
1
2
of another group of
2
3
in
3 wholes.
Note: It is possible to interpret the quotient as how many are in 1 whole. For
example, if there are 3 objects in
2
3
of a unit, there would be 4
1
2
objects in a whole
unit. This interpretation is unlikely in 6
th
grade.
A recipe requires
1
4
lb of onions to make 3 servings of soup. Mark has 1
1
2
lbs
of onions. How many servings can Mark make?
Return to: Standards

NC 6
th
Grade Math Unpacking - Revised June 2022
11
Compute fluently with multi-digit numbers and find common factors and multiples.
NC.6.NS.2 Fluently divide using long division with a minimum of a four-digit dividend and interpret the quotient and remainder in context.
Clarification
Checking for Understanding
This standard introduces the long division process, the standard algorithm for division, for
the first time. To divide fluently, means to operate flexibly, accurately, efficiently and
appropriately. In elementary, students used a variety of methods to divide (repeated
subtraction, equal groups, decomposing using place value, finding greatest multiples,
etc.).
In order to achieve fluency, the student must understand the meaning of division and its
relationship to multiplication and place value. Students are expected to interpret the
quotient and remainder in context. Students should choose an appropriate manner to
write the remainder, using an R, a decimal, or a fraction. Students may encounter
repeating decimals in their work, giving the opportunity to introduce the concept.
Describing the remainder
Example when appropriate
Using R
When needing a count of how many will be left. A group
of 5 friends are dividing up Halloween treats.
Using a decimal
Money, a context using decimals, metric measurements.
Using a fraction
For many customary measurements, a fraction is more
appropriate.
The area is 14
2
. The length is 4. What is the width?
Divide the following:
a) 2600 ÷ 25
b) 1131 ÷ 87
c) 1435 ÷ 164
d) 71,508 ÷ 531
A group of 32 students have raised money to help pay for a field
trip to the Outer Banks Research Park. The trip will cost $3,200
and they have raised $2,156. The students have to pay for the
remaining cost of the trip. How much will each student have to
pay?
Return to: Standards
Compute fluently with multi-digit numbers and find common factors and multiples.
NC.6.NS.3 Apply and extend previous understandings of decimals to develop and fluently use the standard algorithms for addition, subtraction, multiplication
and division of decimals.
Clarification
Checking for Understanding
Students build off of previous understandings to fluently use the standard algorithms for
operations with decimals. Fluently means to operate flexibly, accurately, efficiently and
appropriately.
For addition and subtraction, students use reasoning with place value in the base ten
number system to understand why numbers are placed to align the decimal points.
For multiplication and division, students can use estimation about products and quotients
to determine an algorithm for the placement of the decimal in the quotient or product.
Students use reasoning of the base ten number system and knowledge of multiplying by
tens or tenths to understand the placement of the decimal in the product or quotient.
Evaluate the following:
a) 32.57 + 7.6
b) 14.2 −3.54
c) 23.67
(
5.8
)
d) 2.248 ÷ 5.62
A student claims that the number of decimal places in the product
will always be the same as the total number of decimal places in
the factors. Do you agree or disagree? Explain your reasoning.
Return to: Standards

NC 6
th
Grade Math Unpacking - Revised June 2022
12
Compute fluently with multi-digit numbers and find common factors and multiples.
NC.6.NS.4 Understand and use prime factorization and the relationships between factors to:
● Find the unique prime factorization for a whole number.
● Find the greatest common factor of two whole numbers less than or equal to 100.
● Use the greatest common factor and the distributive property to rewrite the sum of two whole numbers, each less than or equal to 100.
● Find the least common multiple of two whole numbers less than or equal to 12 to add and subtract fractions with unlike denominators.
Clarification
Checking for Understanding
The standard places focus on the relationship between the factors of numbers to be
used as a tool when solving the specific problem types listed in the bullets. In
elementary, students learned to identify primes, composites, and factor pairs.
Note: Students may use their knowledge of multiplication facts to bypass any
procedure to obtain the answer.
Find the unique prime factorization for a whole number.
Students are expected to find the prime factorization of a whole number. Students
learned to distinguish between prime and composite numbers in elementary. To
meet this standard, students:
o Understand that each whole number has a unique prime factorization and
that each prime factorization is unique to each whole number.
o Use exponents to write the prime factorization.
Factor trees and upside-down division are a few ways to organize the prime factors.
For example: Write the prime factorization of 18.
Solution: Using upside down division. Start with the smallest usable prime number, 2, to
divide the 18. This gives a 9. Since 9 is not prime and not divisible by 2, go the
next highest prime number, 3, to divide 9. That produces 3, which is a prime
number. Since this number is no longer divisible by another, the pattern is
complete. Using exponents, the prime factorization is 2 ∙3
2
.
Find the greatest common factor of two whole numbers less than or equal to
100.
Students find the greatest common factor and defend their answer using the prime
factorization of each number.
For example: Find the greatest common factor of 12
and 18.
Solution: The prime factorization of 12 is 2
2
∙3.
The prime factorization of 18 is 2 ∙3
2
.
Using a Venn Diagram: GCF is 6 (product of numbers in the
intersection).
Write the prime factorization of the following numbers:
a) 12
b) 24
c) 10
d) 60
Answer the following questions using your work from the question
above.
e) What is the multiplicative relationship between 12 and 24? How
do you see this in the prime factorization?
f) What is the greatest common factor between 12 and 24?
g) What is the multiplicative relationship between 10 and 60? How
do you see this in the prime factorization? What is the GCF of
10 and 60?
h) What is the greatest common factor between 10 and 24?
Answer the following questions using your work from the question
above.
i) What is the least common multiple of 12 and 10?
j) What is the GCF of 12 and 10?
k) A common factor can always be found by multiplying the two
numbers, in this case 12 ∙10 = 120. However 120 is not the
LCM. Is there a relationship between 120, the GCF of 12 and
10, and the LCM of 12 and 10?
l) Does this relationship work with other numbers? Demonstrate
how this works or does not work.

NC 6
th
Grade Math Unpacking - Revised June 2022
13
Use the greatest common factor and the distributive property to rewrite the
sum of two whole numbers, each less than or equal to 100.
This is the students’ first exposure to the process of factoring. Students use their
skills of finding a GCF to rewrite the sum of two whole numbers using the distributive
property. Students can then demonstrate equivalency of the expression by
evaluating each expression.
For example: Rewrite the following into an equivalent expression, using the
GCF of both numbers and the distributive property: 32 + 54
Solution: 2 ∙16 + 2 ∙27 = 2(16 + 27)
Check for equivalency: 32 + 54 = 86 and 2
(
16 + 27
)
= 2
(
43
)
= 86
Find the least common multiple of two whole numbers less than or equal to 12
to add and subtract fractions with unlike denominators.
Students find the least common multiple and justify their answer using the prime
factorization of each number.
For example: Find the least common multiple of 12 and
8.
Solution: The prime factorization of 12 is 2
2
∙3.
The prime factorization of 8 is 2
3
.
Using a Venn Diagram:
The LCM is 3 ∙2 ∙2 ∙ 2 = 24.
In 5
th
grade, students added and subtracted fractions that are related, meaning that
one of the denominators is a factor of the other. With this limitation, students were
able to change to a like denominator using equivalent fractions, for example knowing
that
1
2
is equivalent to
2
4
.
In 6
th
grade, student will use their new tool, the LCM, to find the least common
denominator, allowing them to add and subtract fractions with any denominator less
than 12.
Rewrite the following into equivalent expressions using the GCF of both
numbers and the distributive property. When complete, evaluate the
expressions to check for equivalency.
a) 16 + 22
b) 12 + 18
c) 36 + 84
d) 13 + 65
Evaluate the following expressions:
a)
6
7
+
1
2
b)
3
4
−
7
10
c) 2
3
8
+ 5
5
6
d) 6
1
3
−2
5
9
Simon is building a triangular picture frame. What length of wood must
he buy to construct the isosceles triangle frame seen in the picture?
Return to: Standards

NC 6
th
Grade Math Unpacking - Revised June 2022
14
Apply and extend previous understandings of numbers to the system of rational numbers.
NC.6.NS.5 Understand and use rational numbers to:
● Describe quantities having opposite directions or values.
● Represent quantities in real-world contexts, explaining the meaning of 0 in each situation.
● Understand the absolute value of a rational number as its distance from 0 on the number line to:
o Interpret absolute value as magnitude for a positive or negative quantity in a real-world context.
o Distinguish comparisons of absolute value from statements about order.
Clarification
Checking for Understanding
This standard introduces students to the concept of negative values.
Describe quantities having opposite directions or values.
Students recognize real-world contexts that have positive and
negative values. For example, students understand that some
quantities can be measured in negative, or opposite values, such as
temperature. For other quantities, this would not be appropriate, such
as the number of students in a classroom.
Represent quantities in real-world contexts, explaining the
meaning of 0 in each situation.
Students understand the meaning of 0 in each context. Understanding
the meaning of zero and positive and negative values in context is
crucial to create and interpret graphs.
Students understand that integers are whole numbers and their
opposites.
In 6
th
grade, students can describe rational numbers as integers,
fractions and decimals. It is not an expectation to define the complete
real number system.
Understand the absolute value of a rational number as its
distance from 0 on the number line
This is the students’ first exposure to absolute value. Students are
expected to describe absolute value as the distance of a number from
zero. Students explain the differences between comparisons of the
absolute value of numbers and comparisons of the numbers
themselves. For example, −7 < 2 but
|
−7
|
>
|
2
|
.
Name three measurements that can have both positive and negative values and
provide an example of a positive and negative value in each context.
Answer the following questions about the three points plotted on the
number line to the right.
a) If the number line represented temperature measured in degrees
Celsius, what does each point represent and describe how it would
feel if that was the temperature outside.
b) If the number line represents your bank account, what would each
point mean?
One morning the temperature is −28℉ in Anchorage, Alaska, and 65℉ in Miami,
Florida. How many degrees warmer was it in Miami than in Anchorage on that
morning?
Describe the following as true or false. If it is false, correct the statement.
a) The farther a number is from zero, the value of the number decreases.
b) The farther a number is from zero, the absolute value of the number increases.
If −3.5 < −3, why is
|
−3.5
|
>
|
−3
|
?
Return to: Standards

NC 6
th
Grade Math Unpacking - Revised June 2022
15
Apply and extend previous understandings of numbers to the system of rational numbers.
NC.6.NS.6 Understand rational numbers as points on the number line and as ordered pairs on a coordinate plane.
a. On a number line:
o Recognize opposite signs of numbers as indicating locations on opposite sides of 0 and that the opposite of the opposite of a number is the number
itself.
o Find and position rational numbers on a horizontal or vertical number line.
b. On a coordinate plane:
o Understand signs of numbers in ordered pairs as indicating locations in quadrants.
o Recognize that when two ordered pairs differ only by signs, the locations of the points are related by reflections across one or both axes.
o Find and position pairs of rational numbers on a coordinate plane.
Clarification
Checking for Understanding
The standard builds upon students’ previous knowledge of number lines and
the coordinate plane. In 6
th
grade, students plot rational numbers on number
lines and coordinate planes.
The Number Line
Using a number line, students demonstrate that they interpret a number as
having both a distance from 0 (magnitude) and a direction (positive or
negative). Students should be exposed to number lines, which include negative
numbers, that are both horizontal and vertical, and build understanding from
real world examples. Students interpret the negative sign as being the “opposite
of.” This reflects the magnitude of the number across 0. Students know that
each iteration of the negative sign reflects the magnitude of the number across
0.
The Coordinate Plane
In previous grades, students were limited to coordinates in the first quadrant. In
6
th
grade, students are expected to identify the quadrant in which an ordered
pair is located and to plot an ordered pair comprised of two rational numbers
based on their understanding of horizontal and vertical number lines.
Students are expected to know that points
(
,
)
and
(
,
)
are reflections of
each other because they are:
● located on the same horizontal line
● equidistant from the y-axis but on opposite sides.
Students are expected to know that points
(
,
)
and
(
,
)
are reflections of
each other because they are:
● located on the same vertical line
● equidistant from the x-axis but on opposite sides.
Place the following on a number line.
a) 3
b) 3
c) 3
d) 3
Use the previous work to answer the following question. What is the absolute
value of each number? How is this possible?
Without graphing coordinates, how can you determine in which quadrant
each point would be located? In which quadrant is each point located?
a) 5
, 6
b) 5
, 6
c)
(
5.5, 6.75
)
d)
(
5.5, 6.75
)
Graph the coordinates from the previous question. How do the locations of
the points relate to each other and the axes?
The point
(
2.1, 3.5
)
is reflected over the x-axis, what is the coordinate of that
point of reflection?
Return to: Standards

NC 6
th
Grade Math Unpacking - Revised June 2022
16
Apply and extend previous understandings of numbers to the system of rational numbers.
NC.6.NS.7 Understand ordering of rational numbers.
a. Interpret statements of inequality as statements about the relative position of two numbers on a number line diagram.
b. Write, interpret, and explain statements of order for rational numbers in real-world contexts.
Clarification
Checking for Understanding
Students are expected to compare and order rational numbers, which in
6
th
grade can be defined as integers, fractions, and decimals. Students
interpret an inequality by describing its position on a number line.
For example: Describe the relationship between the numbers in the
following inequality:
1
3
> .35
Sample solution: Negative one third is greater than negative 35 hundredths.
This means that on a number line negative one third would be to the right of
negative 35 hundredths.
Given a set of rational numbers in a real-world context, students place
the numbers in a particular order, explain their reasoning, and interpret
meaning based on the context.
Place the following points on a number line: 5, 3.5,
, 3, 2
Using the points and number line from the previous question, compare the following
using >, <, or = to describe the relationship between the value of each number.
a) 5_____
b) 3_____ 2
c) 3_____ 3.5
d)
_____ 3
Fill in the blank: If a number is located to the left of another number on the number
line, that number is ______ the other number.
The balance in Sue’s checkbook was –$12.55. The balance in John’s checkbook
was –$10.45. Write an inequality to show the relationship between these amounts.
Who owes more? How do you know?
Return to: Standards
Apply and extend previous understandings of numbers to the system of rational numbers.
NC.6.NS.8 Solve real-world and mathematical problems by graphing points in all four quadrants of the coordinate plane. Include use of coordinates and
absolute value to find distances between points with the same first coordinate or the same second coordinate.
Clarification
Checking for Understanding
Students use the coordinate plane as a tool to solve problems. In
previous grades, students were limited to working in the first quadrant. In
6
th
grade, students will be expected to solve problems using coordinates
that are in different quadrants or on the axes.
Students are expected to find the distance between points on the same
horizontal or same vertical line.
What is the distance between (– 5, 2) and (– 9, 2)?
Rectangle RSTU has vertices at
(
4,3
)
,
(
4, 2
)
, (5, 2) and
(
5,3
)
. Plot the
rectangle on a coordinate plane and find the perimeter of the figure.
The perimeter of a square is 22 units. One of the vertices of the square is located on
the origin of a coordinate plane. One of the vertices is located in the 3
rd
quadrant.
What are the possible coordinates of the vertices of the square?
Return to: Standards
NC 6
th
Grade Math Unpacking - Revised June 2022
17
Apply and extend previous understandings of numbers to the system of rational numbers.
NC.6.NS.9 Apply and extend previous understandings of addition and subtraction.
● Describe situations in which opposite quantities combine to make 0.
● Understand + as the number located a distance q from p, in the positive or negative direction depending on the sign of q. Show that a number and
its additive inverse create a zero pair.
● Understand subtraction of integers as adding the additive inverse, = + (– ). Show that the distance between two integers on the number line is
the absolute value of their difference.
● Use models to add and subtract integers from -20 to 20 and describe real-world contexts using sums and differences.
Clarification
Checking for Understanding
The standard addresses adding and subtracting integers. Students
add and subtract integers between -20 and 20, using models.
Rules are not expected at this grade level. When derived from a
real-world problem, students describe the sum or difference in
context. These problems may require multiple steps. For example,
evaluate 6 + (4) + (3) 7.
Making Zero Pairs
Students are expected to create examples in which a number and
the opposite of that number combine to make zero. Students
describe these numbers as an additive inverse of each other and
recognize that together they make a zero pair.
Adding and Subtracting Integers
Students are expected to interpret integers as having both a
distance and a direction. Students demonstrate this understanding
using a number line to:
● Add integers
o Students interpret the sum as the combination of
distances with their corresponding direction.
o Students explain how additive inverses create a zero
pair.
● Subtract integers
o Students interpret the absolute value of the difference as
the distance between numbers.
o Students explain why they can rewrite subtraction as
addition and use this property as needed.
While students are required to understand addition and subtraction
of integers using number lines, students may use and interpret
other models to find sums and differences or to demonstrate an
understanding of the concepts of this standard. Students may start
using physical models, such as algebra tiles and integer chips. By
the end of the year, students should move to visual models, such
as number lines.
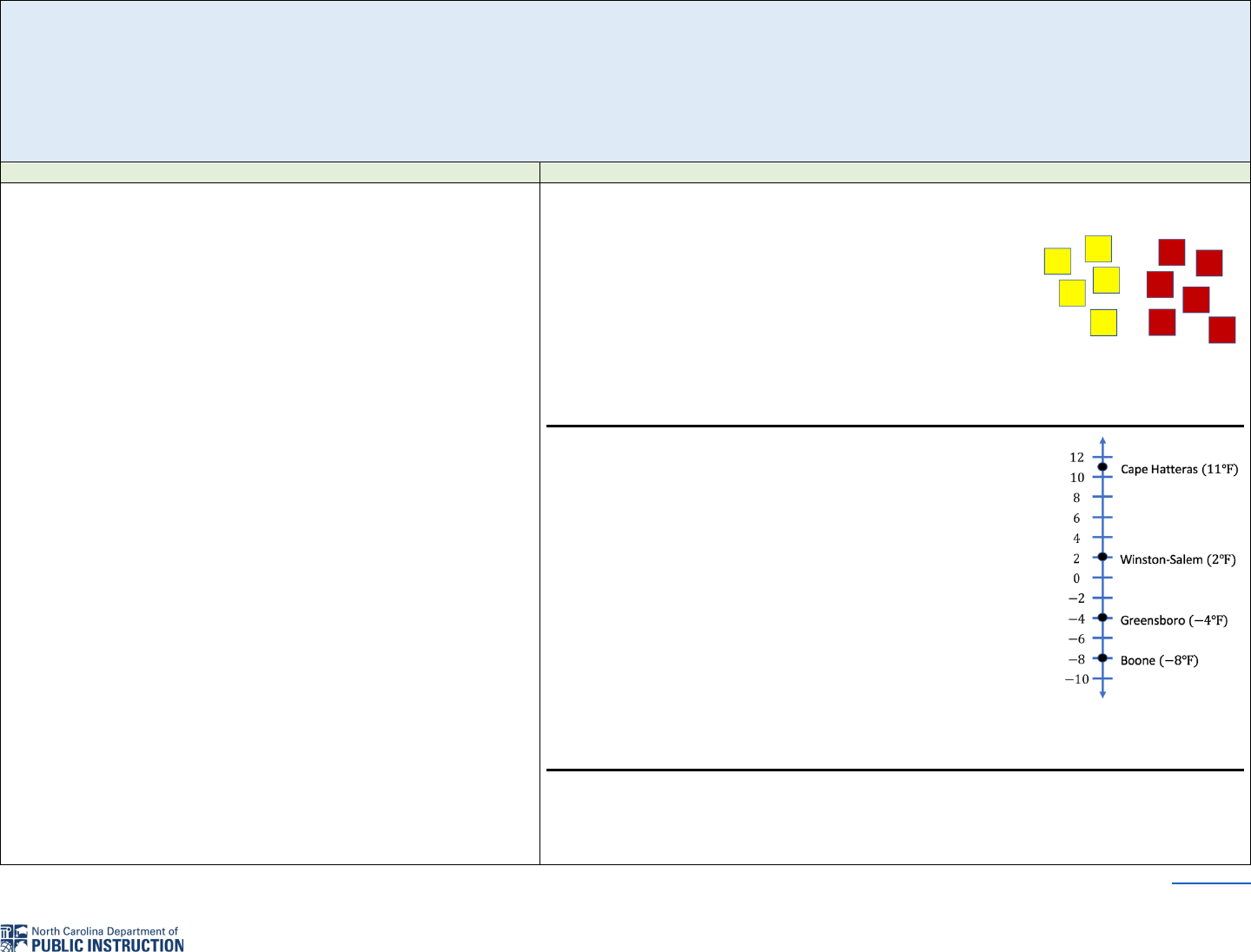
Answer the following questions. A student laid out these squares to represent a positive
and a negative number. Each yellow square represents a positive one while each red
square represents a negative one.
a) What number is represented by the yellow squares?
b) What number is represented by the red squares?
c) How many zero pairs are represented by the yellow and
red squares? How do you know?
d) If the squares represented an addition problem, write an
expression to represent the problem, and what would be
the sum?
The number line shows the record low temperatures for these
North Carolina cities in the month of February.
a) How much warmer was the record low in Cape Hatteras
than the record low in Boone?
b) How much cooler was the record low in Boone than the
record low in Greensboro?
c) How much warmer was the record low in Winston-Salem
than in Greensboro?
d) How much cooler was the record low in Greensboro than
Winston-Salem?
e) A student got the same answer for questions c) and d). The
students shared in a discussion, “I thought that when I was
counting down the number line, I would get a negative
answer, but I got a positive answer no matter which way I
counted.” Explain to the student why all of these answers were positive.
Rewrite the following into equivalent expressions and then evaluate each expression.
a) 5 +
(
3
)
b) 8 17
c) 7 +
(
15
)
d) 4 12
Return to: Standards

NC 6
th
Grade Math Unpacking - Revised June 2022
18
Expressions and Equations
Apply and extend previous understandings of arithmetic to algebraic expressions.
NC.6.EE.1 Write and evaluate numerical expressions, with and without grouping symbols, involving whole-number exponents.
Clarification
Checking for Understanding
The standard places a focus on understanding the evaluation, meaning,
notation, and vocabulary of whole-number exponents. The base of an
expression with an exponent may be any positive rational number.
Students write numerical expressions from verbal and visual
representations that can involve grouping symbols and whole-number
exponents. Students evaluate numerical expressions, using
mathematical reasoning to develop a proper sequence of steps.
Examples of student reasoning:
● multiplication is done before addition because multiplication is
repeated addition
● addition and subtraction are done in the order they are written
because subtraction can be written as addition (See NC.6.NS.9)
In 5
th
grade, only grouping symbols used were parentheses. In 6
th
grade,
grouping symbols may include: parentheses, brackets, braces and
multiple sets of parentheses.
Students understand that parts of an expression have understood
grouping symbols, such as numerators or denominators of fractions.
In the following pictures, using exponents, write an expression that represents the
total number of squares in the picture and then find the total number of squares.
For the question above, describe how you found the total with a partner. What was
the most efficient way to find the total?
Consider the following expressions: 6 + 3
and
(
6 + 3
)
Evaluate each expression and explain why they have different answers.
The expression 4
(
4
)(
8 2
)
and 4
are equivalent.
Show that the two expressions are equivalent. Describe the steps that can be
applied to 4
(
4
)(
8 2
)
to create the equivalent expression 4
.
Taken from: SBAC Mathematics Practice Test Scoring Guide Grade 6 p. 34
What is the value of each expression?
a) 0.2
b)
[
4
(
2 + 3
)]
5
(
30 10
)
c) 7
– 24 ÷ 3 + 26
d) 2
(
1 +
(
5 4
)
)
e)
()
f)
(
5 2
)
g)
h)
(
3.2 1.4
)
Return to: Standards
a)
b)

NC 6
th
Grade Math Unpacking - Revised June 2022
19
Apply and extend previous understandings of arithmetic to algebraic expressions.
NC.6.EE.2 Write, read, and evaluate algebraic expressions.
● Write expressions that record operations with numbers and with letters standing for numbers.
● Identify parts of an expression using mathematical terms and view one or more of those parts as a single entity.
● Evaluate expressions at specific values of their variables using expressions that arise from formulas used in real-world problems.
Clarification
Checking for Understanding
Write expressions that record operations with numbers and with
letters standing for numbers.
Students:
● translate numerical and algebraic expressions from verbal
representations and
● translate given numerical and algebraic expressions using
words.
Identify parts of an expression using mathematical terms and view
one or more of those parts as a single entity.
Students are expected to identify parts of expression, using terms like
constant, coefficient, variable, base, exponent, quantity, sum, difference,
product, factor, quotient, and term.
Students understand that terms such as quantity, sum, difference,
product, and quotient identify multiple parts of an expression that can be
treated as a single entity and often have understood grouping symbols.
Evaluate expressions at specific values of their variables using
expressions that arise from formulas used in real-world problems.
Students evaluate algebraic expressions derived from real-world
problems.
In order to understand a formula, students formalize the definition of an
equation as expressions with equivalent values. This means that if the
value of one expression is found through evaluation, the value of the
other expression is also known.
Students will be able to evaluate formulas in which the algebraic
expressions are limited to two variables in one expression that is set
equal to another variable, for example, =
and = 2+ 2.
Write the following as an algebraic
expression:
a) 7 less than 3 times a number
b) 3 times the sum of a number and 5
c) Twice the cube of
d) The quotient of the sum of x plus 4 and 2
Write the following in words:
e) + 21
f) 6
g)
h)
( + 3)
For parts f) through i), identify at least one example of the following: constant,
coefficient, variable, base, exponent, quantity, sum, difference, product, factor,
quotient, and term.
The formula to find the volume of a cube can be written as =
. The length of the
side of a square of one cube is 5 in., and the length of the side of a square of another
cube is 2 inches longer.
a) What do you expect to be the difference in the volumes of the cubes?
b) Write an expression to represent the volume of each cube.
c) Evaluate the expressions.
d) Was your prediction close? Why was that the case?
You and a friend are traveling to Canada. Watching the weather forecast, you see
the projected high temperature for the day is . You look up the formula to
convert Celsius to Fahrenheit and see that it is =
+ 32. Based on the result of
the formula, what clothes should you pack?
Return to: Standards

NC 6
th
Grade Math Unpacking - Revised June 2022
20
Apply and extend previous understandings of arithmetic to algebraic expressions.
NC.6.EE.3 Apply the properties of operations to generate equivalent expressions without exponents.
Clarification
Checking for Understanding
Students use the properties of operations to rewrite expressions into equivalent
forms. The properties of operation include the commutative, associative, identity
and distributive properties, and combining like terms.
For example: Produce an equivalent expression for 3(2 + ).
Solution: Using the definition of multiplication, students should
see the expression as 3 groups of (2 + ).
As seen in the visual, this produces 3 groups of 2 and 3 groups
of x. Written as multiplication, this is 3 2 + 3 which is 6 + 3.
In this grade level, students are not expected to distribute a variable to an
expression, factor a variable from algebraic expression, or rewrite algebraic
expressions that contain exponents.
Students are planting a flower bed for science class. The flower bed can be
4.5 ft wide and will be divided into 2 sections for roses and irises. The iris
section will be 3 ft long and it has not yet been
determined how long the rose section will be.
a) A student in the class claims that the area of
the flower bed could be written as 4.5
(
+ 3
)
.
Write an equivalent form of this expression.
b) How do you know the two expressions are equivalent?
Write an equivalent expression for 3( + 4) + 2( 2) that has only two
terms.
Use the distributive property to write an equivalent expression for 30+ 18.
Use properties of operations to write at least 3 different expressions
equivalent to each of the following: 6(2+ 3) and 3 + 6 + 9
Return to: Standards
Apply and extend previous understandings of arithmetic to algebraic expressions.
NC.6.EE.4 Identify when two expressions are equivalent and justify with mathematical reasoning.
Clarification
Checking for Understanding
Students show that two algebraic expressions are equivalent, explaining their
steps using mathematical reasoning and mathematical properties. In 6
th
grade,
the focus on showing equivalency of algebraic expressions relies on substituting
the same number for the variable(s) in both expressions and showing that the
resulting values of the expressions are equivalent.
Students notice that this equivalency is not dependent on the number substituted
in for the variable and should work for all numbers. It is also important for
students to check with multiple numbers as some numbers (especially 0, 1, and
2) can lead to a false equivalency claim.
Students may also use the properties of operations to rewrite one expression
into another to show equivalency (see NC.6.EE.3).
Some high school students were disagreeing about their Math 1 homework.
One students claimed that
(
2 3
)
was equivalent to 4
+ 9. The other
students said, no,
(
2 3
)
is equivalent to 4
12 + 9.
Help out these high school students! Who is correct? Explain how you
know.
Return to: Standards

NC 6
th
Grade Math Unpacking - Revised June 2022
21
Reason about and solve one-variable equations.
NC.6.EE.5 Use substitution to determine whether a given number in a specified set makes an equation true.
Clarification
Checking for Understanding
Students use substitution to determine when given numbers make an equation
true and identify this number as a solution of the equation. Students define a true
equation as having the same numerical value on both sides of the equal sign.
Students understand that typically almost all values substituted into an equation
will make it false. Students are not expected to know or use set notation.
Four high school students are working on a Math 1 problem to find the
solution to
(
2 3
)
= 121 Each student got a different answer. The four
answers were 5, 6, 7, and 9.
a) Which of these numbers make the equation true?
b) How do you know?
Return to: Standards
Reason about and solve one-variable equations.
NC.6.EE.6 Use variables to represent numbers and write expressions when solving a real-world or mathematical problem
Clarification
Checking for Understanding
Students interpret a context to write an expression that contains a variable. This
standard deals with writing algebraic expressions beyond direct mathematical
translations (see NC.6.EE.2) and understanding what was written.
Students state, with precision, the meaning of a variable and describe when a
variable, in an expression or equation, represents:
● a single number, often when the expression can be written as an equation
For example: A school is using 12 passenger vans to transport students on a
field trip. With 36 students going on the field trip, how many vans will be
needed?
● all numbers, such as in an expression
For example: It is 12 degrees warmer then yesterday. Write an expression to
represent the temperature today.
● a range of numbers, which in 6
th
grade is limited by interpretation from
context, such as only whole numbers.
For example: A school is using 12 passenger vans to transport students on a
field trip. Write an expression that represent the largest number of students
that can be transported in vans.
Write an expression to represent the following:
a) Susan’s age in three years, when a represents her present age.
b) The number of wheels, w, on any number of bicycles.
c) The value of any number of quarters, q.
Write an expression that represents the following:
a) The skating rink charges $100 to reserve the place and then $5.50
per person. Write an expression to represent the cost for any
number of people.
b) Maria has three more than twice as many crayons as Elizabeth.
Write an algebraic expression to represent the number of crayons
that Maria has.
A school is using 12 passenger vans to transport students on a field trip.
Write an expression to represent the number of vans needed for s
students.
Describe a situation that can be represented by the expression 2c + 3.
Return to: Standards

NC 6
th
Grade Math Unpacking - Revised June 2022
22
Reason about and solve one-variable equations.
NC.6.EE.7 Solve real-world and mathematical problems by writing and solving equations of the form:
● + = in which p, q and x are all nonnegative rational numbers; and,
● ∙ = for cases in which p, q and x are all nonnegative rational numbers
Clarification
Checking for Understanding
Students write and solve one-step equations.
In 6
th
grade, students write equations by first writing an algebraic
expression (see NC.6.EE.6) and then setting it equal to the known value of
the expression.
Many students may find the solution to these basic problems using an
arithmetic process.
For example: A school is using 12 passenger vans to transport
students on a field trip. With 36 students going on the field trip, how
many vans will be needed?
In this question, many students may solve this problem using operations
directly, in this case, = 36 ÷ 12. This means that they start with the end,
36, and work backwards through the problem.
The expectation of the standard is that students will learn to write an
equation to represent this problem, 12 ∙ = 36. This means starting at
beginning and working forward through the problem to the known value of
the expression, using variables to represent unknown quantities.
Students see the relationship between the equation and the arithmetic
process. This leads students to seeing the relationship of inverse
operations and the beginning of an algebraic approach to solving
equations. As problems become more complex, the algebraic approach
becomes the more efficient method to find solutions.
Note: While both = 36 ÷ 12 and 12 ∙ = 36 are equations, to meet the
expectation of this standard, students who write the initial equation with the
variable by itself, should be asked to represent the situation with an
equation like the forms mentioned in the standard.
Students know that the process for finding the number(s) that makes an
equation true, the solution, using mathematical reasoning is called solving.
Students use the skills learned in NC.6.EE.5 to verify they have found the
solution.
While subtraction and division can be used when selecting problems for this
standard, problems involving negative numbers, negative variables, a
variable in the denominator, and complex fractions are beyond the
expectation of this standard.
Meagan spent $56.58 on three pairs of jeans. If each pair of jeans costs the same
amount, write an algebraic equation that represents this situation and solve to
determine how much one pair of jeans cost.
Select all equations that have = 6 as a solution.
A. 2 + = 6
B. + 6 = 12
C. 4 ∙ = 24
D. ∙3 = 2
A fruit salad consists of blueberries, raspberries, grapes, and cherries. The fruit
salad has a total of 280 pieces of fruit. There are twice as many raspberries as
blueberries, three times as many grapes as cherries, and four times as many
cherries as raspberries. How many cherries are there in the fruit salad?
Robert has x books. Marie has twice as many books as Robert has. Together
they have 18 books. Which of the following equations can be used to find the
number of books that Robert has?
A. + 2 = 18
B. + + 2 = 18
C. + 2 = 18
D. 2 = 18
E. 2 + 2 = 18
NAEP – Released Item (2011) Question ID: 2011-8M12 #5 M153101
Solve the following equations:
a) 12 = 8 +
b) −
2
3
=
1
4
c) 2.3 + = 7.1
d) 1
2
5
= ∙
1
6
e)
4
= 3.3
f) 9.5 −2.8 + = 20.2
Return to: Standards

NC 6
th
Grade Math Unpacking - Revised June 2022
23
Reason about one variable inequalities.
NC.6.EE.8 Reason about inequalities by:
● Using substitution to determine whether a given number in a specified set makes an inequality true.
● Writing an inequality of the form x > c or x < c to represent a constraint or condition in a real-world or mathematical problem.
● Recognizing that inequalities of the form x > c or x < c have infinitely many solutions.
● Representing solutions of inequalities on number line diagrams.
Clarification
Checking for Understanding
Students interpret inequalities and use them to describe situations.
Since students can already determine equality, this standard includes
the use of
≥, ≤, > or < throug hout. The use of ≤ a nd ≥ a re new to
s tu d e n ts .
Using substitution to determine whether a given number in a
specified set makes an inequality true.
Students identify the solutions of inequalities of the form ≥ or ≤
when c is either positive or negative. Students also determine if c is
included in the solutions.
Writing an inequality of the form x > c or x < c to represent a
constraint or condition in a real-world or mathematical problem.
Students use reasoning to determine the appropriate inequality to use in
a given situation. For example, a person must be at least 16 years old to
obtain a driver’s license.
Recognizing that inequalities of the form x > c or x < c have
infinitely many solutions.
Students recognize the relationship between an infinite number of
solutions and the need to shade number lines to represent these infinite
solutions.
Representing solutions of inequalities on number line diagrams.
Students represent inequalities on a number line, using appropriate
symbols. Students are also expected to write an inequality from its
graphical representation.
In 6
th
grade, students are not expected to solve inequalities or to write
compound inequalities.
Consider the following numbers: −3.25, −2, 3.5, 4, 4
2
3
, 5
Which of these numbers are a possible solution to the following inequalities?
a) ≤ 3
1
2
b) −2 >
c) ℎ ≥ −3.2
d) 4 <
Consider the following numbers: −3, −2, 3, 4, 5
Which of these numbers are a possible solution to the following inequality?
2( + 3) ≤ 1
Write an inequality to represent each situation.
a) The Flores family spent less than $400.00 last month on groceries.
b) The class must raise at least $100 to go on the field trip.
c) In order to get an attendance award, a student can have at most 2 absences
for the year.
A student wrote 1.75 to represent the cost of sports drinks with d representing the
number of drinks. Write an inequality that describes possible values for d. Explain.
Create a number line that represents the following inequalities.
a) ≤ 3
1
2
b) −2 >
c) ℎ ≥ −3.2
d) 4 <
Write the inequality represented in the
graph.
Return to: Standards

NC 6
th
Grade Math Unpacking - Revised June 2022
24
Represent and analyze quantitative relationships between dependent and independent variables.
NC.6.EE.9 Represent and analyze quantitative relationships by:
● Using variables to represent two quantities in a real-world or mathematical context that change in relationship to one another.
● Analyze the relationship between quantities in different representations (context, equations, tables, and graphs).
Clarification
Checking for Understanding
Students describe and analyze how one variable changes in relation to the other.
Using variables to represent two quantities in a real-world or mathematical
context that change in relationship to one another.
Students analyze the relationship between variables in a given situation and
represent that situation as a two-variable equation. Students may be given a partially
completed table or graph along with the context of the situation.
In 6
th
grade, students write an expression from a context and set that expression
equal to a variable that represents the value of the created expression (output). This
variable will be in a dependent relationship to the variable in the created algebraic
expression. From this, students can describe the mathematical relationship between
the variables.
For example: The cost to get into a high school basketball game is $5 for each
ticket. Write an equation to represent this situation and describe the relationship
between the variables.
Solution: Sample answer: = 5 ∙
Possible description: As the number of tickets increases by 1, the cost increases 5 dollars.
is in a dependent relationship to .
Analyze the relationship between quantities in different representations
(context, equations, tables, and graphs).
Students create tabular and graphical representations of equations. In 6
th
grade,
students are expected to create the graphical representation from the corresponding
tabular representation. Student can use a tabular or graphical representation to
analyze the relationship between variables. Students can then relate their finding
back to the equation and the context.
Students understand that:
● A table is an organized list of solutions to its corresponding equation.
● A graph is a visual representation of the solutions to its corresponding
equation.
From the context, equation, or graph, students determine which variable is in a
dependent relationship. Students recognize that on a coordinate plane, the variable
that is in a dependent relationship is graphed on the y-axis. From the example above,
since cost, , is in a dependent relationship with tickets, , cost would be graphed on
the y-axis and tickets would be graphed on the x-axis.
In 6
th
grade, the relationships analyzed should focus on proportional and linear
relationships. Students are not required to use the terms proportional or linear at this
level. The restrictions placed on ratios tables apply to this standard. The initial values
given should be whole numbers.
Chris and his friends are going to the ice cream shop that is having a
sale on milkshakes. Each milkshake cost $2.
a) Write an equation that represents the total cost of buying any
number of milkshakes for Chris and his friends.
b) Create a table and a graph to represent this situation.
c) Describe how the variables relate to each other and explain how
you see these relationships in the equation, table and graph.
The student government is hosting a breakfast for charity and they
need to know how many people will attend so they can make plans.
The four members of the student government will attend the breakfast
along with the number of people who bought a ticket.
a) Write an equation that represents the total attending the
breakfast.
b) Create a table and a graph to represent this situation.
c) Describe how the variables relate to each other and explain how
you see these relationships in the equation, table and graph.
Looking at the two tables created in the
previous examples. One table contains
equivalent ratios, the other does not. How
could you have determined this from the
equations written?
A traveling basketball team is selling candy
bars to raise money for new uniforms. There
are 36 candy bars in each box and each
candy bar costs $1.75 each. The team sold
20 boxes.
a) Complete the table that shows how
much money was collected for each
box.
b) Create an equation to represent the
amount of money collected based on
the number of boxes sold.
c) Graph the equation from the ordered
pairs in the table.
Return to: Standards

NC 6
th
Grade Math Unpacking - Revised June 2022
25
Geometry
Solve real-world and mathematical problems involving area, surface area, and volume.
NC.6.G.1 Create geometric models to solve real-world and mathematical problems to:
● Find the area of triangles by composing into rectangles and decomposing into right triangles.
● Find the area of special quadrilaterals and polygons by decomposing into triangles or rectangles.
Clarification
Checking for Understanding
This standard builds on student understanding of area as the number of
squares needed to cover a plane figure and an understanding of composite
shapes from triangles and rectangles. Students have found the area of
rectangles in the elementary grades. They have also worked with
composite shapes of triangles and rectangles.
Additionally, the process of finding the area of special quadrilaterals and
polygons should include composing and decomposing triangles or
rectangles.
Find the area of a right triangle below.
Show how you can find the area of the isosceles trapezoid shown below by
decomposing into triangles and rectangles and using their area formulas to find
the total area of the figure.
A rectangle measures 3 inches by 4 inches. If the lengths of each side double,
compare the area of the new rectangle to the area of the original rectangle?
Describe visually and or verbally how you arrived at your answer.
Return to: Standards
For example, a trapezoid can be decomposed into triangles and rectangles
(see figures below). Using the trapezoid’s dimensions, the area of the individual
triangle(s) and rectangle can be found and then added together. Special
quadrilaterals include rectangles, squares, parallelograms, trapezoids, rhombi,
and kites.
Finding the area of triangles is introduced in relationship to the area of
rectangles – a rectangle can be decomposed into two congruent
triangles. Students will use this understanding in future grades to find
the area of polygons.
The area of the triangle is ½ the area of the rectangle. The area of a
rectangle can be found by multiplying base and height; therefore, the
area of the triangle is
1
2
ℎ.
h
b
h
b
h
b
Isosceles
trapezoid
Decomposed into a rectangle and 2
congruent triangles.
3
4
5
12
8
3

NC 6
th
Grade Math Unpacking - Revised June 2022
26
Solve real-world and mathematical problems involving area, surface area, and volume.
NC.6.G.2 Apply and extend previous understandings of the volume of a right rectangular prism to find the volume of right rectangular prisms with fractional edge
lengths. Apply this understanding to the context of solving real-world and mathematical problems.
Clarification
Checking for Understanding
This standard builds on previous understanding of volume of right rectangular
prisms. Students previously worked with volume of right rectangular prisms
with whole number edges by packing unit cubes into the figure to build
understanding of the volume formula for rectangular prisms (NC.5.MD.4 and
NC.5.MD.5).
Students will use what they know about fractions, specifically unit fractions, to
decompose the visual image into cubes with unit fractional edge lengths
connecting to multiplication of fractions. This process is similar to composing
and decomposing two-dimensional shapes.
A right rectangular prism has edges of 1
1
4
", 1" and 1
1
2
". How many cubes with
side lengths of
1
4
would be needed to fill the prism? What is the volume of the
prism? (Note: The small unit cube is
1
4
×
1
4
×
1
4
).
Each smaller cube within the 3 × 3 cube below has a side length of
3
4
in. What
is the volume of the 3 × 3 cube?
The toy manufacturer is looking for a box to package the cubes in for shipping.
Which company, A or B, will allow them to send more cubes? Explain your
response. How many cubes can be packaged?
Width
Length
Height
Company A
18”
12”
28”
Company B
16”
24”
20”
Return to: Standards
For example, the model shows a rectangular prism with dimensions
3
2
,
5
2
,
and
5
2
inches. Each of the cubic units in the model is
1
2
inch on each side.
Students work with the model to illustrate
3
2
×
5
2
×
5
2
= (3 × 5 × 5) ×
1
8
.
Students reason that a small cube has volume of
1
8
3
because 8 of them
fit in a unit cube. Students recognize that there are 75 small cubes in the
prism and if 8 of them make a unit cube, then there are 9 unit cubes and
3 small cubes in the prism, so 9
3
8
is a way to express the volume in cubic
units.
3
2
5
2
5
2
3 ×
1
2
unit cubes
5 ×
1
2
unit cubes
5 ×
1
2
unit cubes

NC 6
th
Grade Math Unpacking - Revised June 2022
27
Solve real-world and mathematical problems involving area, surface area, and volume.
NC.6.G.3 Use the coordinate plane to solve real-world and mathematical problems by:
● Drawing polygons in the coordinate plane given coordinates for the vertices.
● Using coordinates to find the length of a side joining points with the same first coordinate or the same second coordinate.
Clarification
Checking for Understanding
This standard connects shapes in the geometry standards to the coordinate
system. Students have plotted points on the coordinate plane. The
coordinate grid creates a good visual for examining properties of polygonal
figures.
Students will draw polygons in the coordinate plane and calculate distances
for vertical and horizontal lines in the plane to solve a variety of problems.
If the points on the coordinate plane are the three vertices of a rectangle, what
are the coordinates of the fourth vertex? How do you know? What are the length
and width of the rectangle? Find the area and the perimeter of the rectangle.
Extension: Can the shape be identified as something other than a rectangle?
Why or why not?
On a map, the library is located at (−2, 2), the city hall building is located at (0,2),
and the high school is located at (0,0). Represent the locations as points on a
coordinate grid with a unit of 1 mile.
1. What is the distance from the library to the city hall building? What is the
distance from the city hall building to the high school? How do you know?
2. What shape does connecting the three locations form? The city council is
planning to place a city park in this area. How large is the area of the planned
park?
Return to: Standards
For example, parallelogram
has vertices
(
−2, 1
)
,
(
−4, −3
)
,
(
2, −3
)
, and
(
4, 1
)
. S
tudents can plot the points
in the coordinate grid and use the
formula for the area of a
parallelogram ( = ℎ) to find the
area of the figure.
So, = 6 × 4 = 24 units
2
Students can also use what they
know about composite figures to
verify the area for the parallelogram.
This standard can be used to assist in
the development of the understanding
for determining the area formula for a
triangle and other special
quadrilaterals.
= 6
ℎ = 4

NC 6
th
Grade Math Unpacking - Revised June 2022
28
Solve real-world and mathematical problems involving area, surface area, and volume.
NC.6.G.4 Represent right prisms and right pyramids using nets made up of rectangles and triangles, and use nets to find the surface area of these figures.
Apply these techniques in the context of solving real world and mathematical problems.
Clarification
Checking for Understanding
This standard helps students to develop their visualization skills by
examining polyhedrons (a 3-dimensional shape with multiple faces made of
polygons) using nets. A net is a two-dimensional representation of a three-
dimensional figure. Students use nets to represent right prisms and
pyramids, figures composed of rectangles and triangles. Nets help students
to examine attributes of prisms and pyramids. They can determine the
shapes of the lateral edges of the figure, the base, and attributes of lines
and angles within the figure.
Using the dimensions of the individual faces, students calculate the area of
each rectangle and/or triangle and add them together to find the surface
area of the figure.
Students visualize and describe the types of faces needed to create a
three-dimensional figure. They also make and test conjectures to determine
what shapes create specific three-dimensional figures.
Describe the shapes of the faces needed to construct a rectangular pyramid.
Draw the net of the figure and label the sides and the bases.
Create the net for a given prism or pyramid, and then use the net to calculate the
surface area.
Return to: Standards
For example, the following is a triangular prism and its corresponding net. The
area of the base is 43.3
2
. The base length of each side and the height of
each side is given enabling students to determine the area of each side as =
1
2
10
(
12
)
= 60
2
. So, the surface area (SA) is = 43.3 + 3
(
60
)
= 223
2
.

NC 6
th
Grade Math Unpacking - Revised June 2022
29
Statistics and Probability
Develop understanding of statistical variability.
NC.6.SP.1
Recognize a statistical question as one that anticipates variability in the data related to the question and accounts for it in the answers.
Clarification
Checking for Understanding
The intention of this standard is the distinction between a statistical question and a non-
statistical question and to begin the discussion of variability and its role in statistical problem
solving. Beginning with a working definition of statistics…
Statistics is a collection of procedures and principles for gaining and analyzing
information in order to help people make decisions when faced with uncertainty
(Utts, 2005).
Students know that a statistical question is one that collects information addressing the
differences (variability) in a population. Students can also differentiate a statistical question
from a research question. Research questions are answered from statistical analysis of data;
therefore, research questions form the basis for the information that will be collected. They are
based on a hypothesized outcome that is supported or refuted through analysis of the data.
For example, the question, “How tall am I?” is NOT a statistical question because there is
only one response; however, the question, “How tall are the students in my class?” is a
statistical question because it anticipates [natural] variability in student heights.
Students understand that variability means that outcomes of data collection may be different
and that statistics is a tool to explain the variability. Students understand that variation in data
can be natural (due to differences in the population) or induced (by data collection). As
students encounter statistics throughout middle school and high school, they will address
variability at higher levels of complexity.
In 6
th
grade, students will focus on natural variability within a group. They will also examine
how variability is induced through data collection and measurement (NC.6.SP.5).
Students are NOT expected to list or name the types of variability, but they should be familiar
with variability as a natural part of the statistical problem-solving process.
Which of the following represent a statistical question? Select
all that apply. Explain.
1. What teaching styles are used by teachers for managing
the behavior of students in this middle school?
2. How many hours per week, on average, do students in our
school exercise outside of school activities?
3. Who has the longest name in our class?
4. What was the temperature this morning at 6 am at Raleigh-
Durham International Airport?
5. Does getting fewer than eight hours of sleep the night
before a standardized exam make 6
th
graders more likely to
do poorly on their EOGs at Middletown Middle School?
6. How many aunts and uncles do you have?
7. What proportion of students at your school eat cold pizza?
8. What is the relationship between playing AAU basketball in
elementary school and making the varsity basketball team
in high school?
Collect data and create statistical questions.
● Explain the difference between a statistical question
and a non-statistical question.
● Create a class survey collecting both categorical and
numerical data. Create at least 3 statistical questions
that can be addressed by the data collected.
Return to: Standards

NC 6
th
Grade Math Unpacking - Revised June 2022
30
Develop understanding of statistical variability.
NC.6.SP.2 Understand that a set of data collected to answer a statistical question has a distribution which can be described by its center, spread, and overall
shape.
Clarification
Checking for Understanding
This standard supports mathematics as a tool to quantify and describe
numerical data that has been generated from a statistical question. In 6
th
grade, students will ONLY calculate measures of center (mean and median) of
a distribution.
Students will use graphical displays to describe the spread and shape of the
data based on visual characteristics of the representations; therefore, it is
important that students have graphed distributions to fully meet this standard.
Key observations include: data clusters (mode), overall width (spread) of the
values, data values that stand out from the rest (outliers), etc. Students do not
need to formally determine the range of the data; however, they should be
able to discuss the specific values in which the data falls in context.
Students are expected to describe a data set given in various forms, this
includes raw data or graphical displays of data. If students are presented with
a graphical display of data, they are expected to know what information
can/cannot be determined from the display (NC.6.SP.4).
Students in Ms. Flowers’ 6
th
grade science class were studying insects and
wanted to know the average length of a red work ant. As a class, they
measured the length of red work ants and displayed the data in the following
histogram.
a. Describe the distribution.
b. What information does the graph give us about the group of red work ants
in the sample?
Ms. Williams wanted information about how well her students were performing
on their mid-semester exam. She created a box plot using their test scores.
Using the graph, decide what information she can determine about her class’
performance on the test.
Return to: Standards
For example, the graph shows the
length of American League Baseball
Team Names. Possible observations
include:
The range of all name lengths.
The length of most names (mode).
The mean and/or median name
lengths.
The idea here is for students to make
their own observations based on the
context and the graph.

NC 6
th
Grade Math Unpacking - Revised June 2022
31
Develop understanding of statistical variability.
NC.6.SP.3 Understand that both a measure of center and a description of variability should be considered when describing a numerical data set.
a. Determine the measure of center of a data set and understand that it is a single number that summarizes all the values of that data set.
o Understand that a mean is a measure of center that represents a balance point or fair share of a data set and can be influenced by the presence of
extreme values within the data set.
o Understand the median as a measure of center that is the numerical middle of an ordered data set.
b. Understand that describing the variability of a data set is needed to distinguish between data sets in the same scale, by comparing graphical
representations of different data sets in the same scale that have similar measures of center, but different spreads.
Clarification
Checking for Understanding
This standard defines the descriptive statistics that students will use to summarize
data distributions at this grade level. Students will use mean and median to describe
measures of center in the middle grades. Students are not expected to calculate
measures of variability; however, they should examine graphical displays of data to
compare data sets with the same center to help them understand the importance of
examining variability between different data sets when analyzing data.
Center: This standard focuses on building conceptual understanding of the mean of a
data set. Students develop understandings of the mean by redistributing data sets to
be level or fair (equal distribution) and by observing that the total distance of the data
values above the mean is equal to the total distance of the data values below the
mean (balancing point).
Students also recognize that the median is the actual data value (for an odd data set)
that falls in the middle of the data set when the data is in order, noting that they have
to calculate the mean of the middle two data values for an even data set.
Emphasis should be placed on the differences in the mean and median in terms of
how they are determined and to what extent their values influence the measurement
of the statistic (mean or median).
Variability: Students understand that measures of center, alone, are insufficient
summaries for statistical data. Variability is as important as measures of center when
analyzing and describing data. Students are not required to calculate measures of
variability in 6
th
grade; however, they should recognize that when data sets have the
same mean that variability can be used to distinguish the data sets.
The diagram below shows the Test Scores for a 6
th
grade mathematics
class. Without performing any calculations, use the graph below to
show how you know that the mean and median test scores are both 92.
The graphs below show the test scores of two students. Who is the
more consistent student? Why is it inappropriate to use the mean
ONLY to help us decide? Explain your reasoning.
Return to: Standards
The mean is 9.

NC 6
th
Grade Math Unpacking - Revised June 2022
32
Summarize and describe distributions.
NC.6.SP.4 Display numerical data in plots on a number line.
● Use dot plots, histograms, and box plots to represent data.
● Compare the attributes of different representations of the same data.
Clarification
Checking for Understanding
Students are expected to use dot plots, histograms and box plots to display
numerical data. They are also expected to compare different types of
representations for a given data set noting the advantages and disadvantages
for using particular representations. Visual and numerical comparisons should
be included. Students should also understand how measures of center and
variability are represented by graphical displays and which displays reveal
specific information (actual data values, number of data, mean, median,
minimum, maximum, shape – symmetrical or skewed, etc.) relating to the data.
Students have created bar graphs and line plots in previous grade levels. Line
plots are very similar to dot plots in that they represent the count of specific
data values along a consistent scale on a horizontal axis. Histograms, not to
be confused with bar graphs, and box plots are new content in the 6
th
grade
standards.
Students can use a variety of methods and tools to create graphical displays,
including but not limited to, by hand, applets, computer programs, or
calculators.
Sample Applets:
● Box Plot Tool – http://illuminations.nctm.org/ActivityDetail.aspx?ID=77
● Histogram Tool – http://illuminations.nctm.org/ActivityDetail.aspx?ID=78
Students do need to know the quartiles to create a box-plot. However, they are
NOT expected to use the interquartile range (IQR) to quantify and interpret
variability.
A class of grade 6 students were collecting data for a class math project.
They decided they would survey the other two 6
th
grade classes to
determine how many DVDs each student owns. A total of 38 students
were surveyed. The data are shown in the table below in no specific
order.
11
21
5
12
10
31
19
13
23
33
10
11
25
14
34
15
14
29
8
5
22
26
23
12
27
4
25
15
7
2
19
12
39
17
16
15
28
16
1) Create two different data displays to organize the data.
2) Describe the shape, center and spread of the distribution.
3) What attributes of the data can you easily see in each of the chosen
displays? Which values can you approximate?
Return to: Standards

NC 6
th
Grade Math Unpacking - Revised June 2022
33
Summarize and describe distributions.
NC.6.SP.5 Summarize numerical data sets in relation to their context.
a. Describe the collected data by:
● Reporting the number of observations in dot plots and histograms.
● Communicating the nature of the attribute under investigation, how it was measured, and the units of measurement.
b. Analyze center and variability by:
● Giving quantitative measures of center, describing variability, and any overall pattern, and noting any striking deviations.
● Justifying the appropriate choice of measures of center using the shape of the data distribution.
Clarification
Checking for Understanding
As students further develop their understanding of variability, they describe
and analyze numerical data based on various representations of data.
Students can identify the attributes of data represented in dot plots and
histograms to quantitatively and qualitatively summarize distributions
(NC.6.SP.4).
Students will use the shape of the data distribution to determine the
appropriate measure of center to quantitatively describe the distribution.
Students understand that symmetrical data displays reflect an “ideal” situation
where the measures of center (mean and median) have very similar values.
Furthermore, students understand that a skewed
distribution is reflected by a visible and calculable difference between the
mean and median. Additionally, students understand the effect of extreme
values on the mean and median and can explain their choice of which
measure more appropriately describes the center of a data distribution:
● Mean is appropriate to use with symmetrical distributions
● Median is appropriate for non-symmetrical distributions and/or
distributions with extreme data values.
Students need to be familiar with various types of shapes, including but not
limited to unimodal, bimodal/multimodal, uniform, and skewed distributions.
A. Skewed left
B. Symmetrical, unimodal
C. Skewed right
D. Bimodal/multimodal
E. Uniform
During the winter, schools are often closed due to severe weather. Sometimes
schools have to make up for the missed days. A local school district wanted to
look at historical data on the number of days missed due to inclement weather.
The following graph shows the frequency distribution of the number of days
missed due to snow storms per year.
a. Approximately how many years of data were collected and analyzed? Use
the graph to show how you came up with your answer.
b. Describe the shape of the data. Does there appear to be any data values
that are outside of the normal pattern of the data? If so, what are they and
what do they mean?
c. What are the mean and the median of the data? What do they tell us about
the data? Which measure is a better descriptor as the measure of center?
Why?
Return to: Standards
