6.045: Automata, Computability, and
Complexity
Or, Great Ideas in Theoretical
Computer Science
Spring, 2010
Class 10
Nancy Lynch
Today
• Final topic in computability theory: Self-Reference
and the Recursion Theorem
• Consider adding to TMs (or programs) a new,
powerful capability to “know” and use their own
descriptions.
• The Recursion Theorem says that this apparent
extra power does not add anything to the basic
computability model: these self-referencing
machines can be transformed into ordinary non-
self-referencing TMs.
Today
• Self-Reference and the Recursion Theorem
• Topics:
– Self-referencing machines and programs
– Statement of the Recursion Theorem
– Applications of the Recursion Theorem
– Proof of the Recursion Theorem: Special case
– Proof of the Recursion Theorem: General case
• Reading:
– Sipser, Section 6.1
Self-referencing machines and
programs
Self-referencing machines/programs
• Consider the following program P
1
.
•P
1
:
– Obtain < P
1
>
–Output < P
1
>
•P
1
simply outputs its own representation, as a
string.
• Simplest example of a machine/program that uses
its own description.
Self-referencing machines/programs
• A more interesting example:
•P
2
: On input w:
– If w = ε then output 0
–Else
• Obtain < P
2
>
• Run P
2
on tail(w)
• If P
2
on tail(w) outputs a number n then output n+1.
• What does P
2
compute?
• It computes |w|, the length of its input.
• Uses the recursive style common in LISP, Scheme, other
recursive programming languages.
• We assume that, once we have the representation of a
machine, we can simulate it on a given input.
• E.g., if P
2
gets < P
2
>, it can simulate P
2
on any input.
Self-referencing machines/programs
• One more example:
•P
3
: On input w:
– Obtain < P
3
>
– Run P
3
on w
–If P
3
on w outputs a number n then output n+1.
• A valid self-referencing program.
• What does P
3
compute?
• Seems contradictory: if P
3
on w outputs n then P
3
on w outputs n+1.
• But according to the usual semantics of recursive
calls, it never halts, so there’s no contradiction.
•P
3
computes a partial function that isn’t defined
anywhere.
Statement of the Recursion
Theorem
The Recursion Theorem
• Used to justify self-referential programs like P
1
, P
2
,
P
3
, by asserting that they have corresponding
(equivalent) basic TMs.
• Recursion Theorem (Sipser Theorem 6.3):
Let T be a TM that computes a (possibly partial) 2-
argument function t: Σ* ×Σ* →Σ*.
Then there is another TM R that computes the
function r: Σ* →Σ*, where for any w, r(w) = t(<R>,
w).

The Recursion Theorem
• Recursion Theorem: Let T be a TM that computes a
(possibly partial) 2-argument function t: Σ* ×Σ* →Σ*. Then
there is another TM R that computes the function r: Σ* →
Σ*, where for any w, r(w) = t(<R>, w).
• Thus, T is a TM that takes 2 inputs.
• Think of the first as the description of
some arbitrary 1-input TM M.
• Then R behaves like T, but with the
first input set to <R>, the description
of R itself.
• Thus, R uses its own representation.
T
<M>
w
t(<M>, w)
R
t(<R>, w)
w

The Recursion Theorem
• Recursion Theorem: Let T be a TM that computes a
(possibly partial) 2-argument function t: Σ* ×Σ* →Σ*. Then
there is another TM R that computes the function r: Σ* →
Σ*, where for any w, r(w) = t(<R>, w).
• Example: P
2
, revisited
– Computes length of input.
– What are T and R?
– Here is a version of P
2
with an extra
input <M>:
–T
2
: On inputs <M> and w:
• If w = ε then output 0
• Else run M on tail(w); if it outputs n then
output n+1.
T
<M>
w
t(<M>, w)
R
t(<R>, w)
w

The Recursion Theorem
• Example: P
2
, revisited
–T
2
: On inputs <M> and w:
• If w = ε then output 0
• Else run M on tail(w); if it outputs n then output
n+1.
–T
2
produces different results, depending
on what M does.
– E.g., if M always loops:
•T
2
outputs 0 on input w = ε and loops on every
other input.
– E.g., if M always halts and outputs 1:
•T
2
outputs 0 on input w = ε and outputs 2 on
every other input.
T
<M>
w
t(<M>, w)
R
t(<R>, w)
w

The Recursion Theorem
• Example: P
2
, revisited
–T
2
: On inputs <M> and w:
• If w = ε then output 0
• Else run M on tail(w); if it outputs n then output
n+1.
– Recursion Theorem says there is a TM R
computing t(<R>, w)---just like T
2
but with
input <M> set to <R> for the same R.
– This R is just P
2
as defined earlier.
T
<M>
w
t(<M>, w)
R
t(<R>, w)
w

The Recursion Theorem
• Recursion Theorem (Sipser
Theorem 6.3):
Let T be a TM that computes a
(possibly partial) 2-argument
function t: Σ* ×Σ* →Σ*.
Then there is another TM R that
computes the function r: Σ* →Σ*,
where for any w, r(w) = t(<R>, w).
T
<M>
w
t(<M>, w)
R
t(<R>, w)
w
Applications of the Recursion
Theorem
Applications of Recursion Theorem
• The Recursion Theorem can be used to show various
negative results, e.g., undecidability results.
• Application 1: Acc
TM
is undecidable
– We already know this, but the Recursion Theorem provides a new
proof.
– Suppose for contradiction that D is a TM that decides Acc
TM
.
– Construct another machine R using self-reference (justified by the
Recursion Theorem):
• R: On input w:
– Obtain < R > (using Recursion Theorem)
– Run D on input <R, w> (we can construct <R, w> from <R> and w)
– Do the opposite of what D does:
• If D accepts <R, w> then reject.
• If D rejects <R, w> then accept.
Application 1: Acc
TM
is undecidable
• Suppose for contradiction that D decides Acc
TM
.
• R: On input w:
– Obtain < R >
– Run D on input <R, w>
– Do the opposite of what D does:
• If D accepts <R, w> then reject.
• If D rejects <R, w> then accept.
• RT says that TM R exists, assuming decider D exists.
• Formally, to apply RT, use the 2-input machine T:
• T: On inputs <M> and w:
– Run D on input <M, w>
– Do the opposite of what D does:
• If D accepts <M, w> then reject.
• If D rejects <M, w> then accept.
Application 1: Acc
TM
is undecidable
• Suppose for contradiction that D decides Acc
TM
.
• R: On input w:
– Obtain < R >
– Run D on input <R, w>
– Do the opposite of what D does:
• If D accepts <R, w> then reject.
• If D rejects <R, w> then accept.
• Now get a contradiction:
– If R accepts w, then
• D accepts <R, w> since D is a decider for Acc
TM
, so
• R rejects w by definition of R.
– If R does not accept w, then
• D rejects <R, w> since D is a decider for Acc
TM
, so
• R accepts w by definition of R.
• Contradiction. So D can’t exist, so Acc
TM
is undecidable.
Applications of Recursion Theorem
• Application 2: Acc01
TM
is undecidable
– Similar to the previous example.
– Suppose for contradiction that D is a TM that decides
Acc01
TM
.
– Construct another machine R using the Recursion
Theorem:
• R: On input w: (ignores its input)
– Obtain < R > (using RT)
– Run D on input <R>
– Do the opposite of what D does:
• If D accepts <R> then reject.
• If D rejects <R> then accept.
• RT says that R exists, assuming decider D exists.
Application 2: Acc01
TM
is undecidable
• Suppose for contradiction that D decides Acc01
TM
.
• R: On input w:
– Obtain < R >
– Run D on input <R>
– Do the opposite of what D does:
• If D accepts <R> then reject.
• If D rejects <R> then accept.
• Now get a contradiction, based on what R does on input 01:
– If R accepts 01, then
• D accepts <R> since D is a decider for Acc01
TM
, so
• R rejects 01 (and everything else), by definition of R.
– If R does not accept 01, then
• D rejects <R> since D is a decider for Acc01
TM
, so
• R accepts 01 (and everything else), by definition of R.
• Contradiction. So D can’t exist, so Acc01
TM
is undecidable.
Applications of Recursion Theorem
• Application 3: Using Recursion Theorem to prove
Rice’s Theorem
– Rice’s Theorem: Let P be a nontrivial property of
Turing-recognizable languages. Let M
P
= { < M > | L(M)
∈ P }. Then M
P
is undecidable.
– Nontriviality: There is some M
1
with L(M
1
) ∈ P, and
some M
2
with L(M
2
) ∉ P.
– Implies lots of things are undecidable.
– We already proved this; now, a new proof using the
Recursion Theorem.
– Suppose for contradiction that D is a TM that decides
M
P
.
– Construct machine R using the Recursion Theorem:…
Application 3: Using Recursion
Theorem to prove Rice’s Theorem
• Rice’s Theorem: Let P be a nontrivial property of Turing-
recognizable languages. Let M
P
= { < M > | L(M) ∈ P }.
Then M
P
is undecidable.
• Nontriviality: L(M
1
) ∈ P, L(M
2
) ∉ P.
• D decides M
P
.
• R: On input w:
– Obtain < R >
– Run D on input <R>
– If D accepts <R> then run M
2
on input w and do the same thing.
– If D rejects <R> then run M
1
on input w and do the same thing.
•M
1
and M
2
are as above, in the nontriviality definition.
• R exists, by the Recursion Theorem.
• Get contradiction by considering whether or not L(R) ∈ P:
Application 3: Using Recursion
Theorem to prove Rice’s Theorem
• Rice’s Theorem: Let P be a nontrivial property of Turing-
recognizable languages. Let M
P
= { < M > | L(M) ∈ P }.
Then M
P
is undecidable.
•L(M
1
) ∈ P, L(M
2
) ∉ P.
• D decides M
P
.
• R: On input w:
– Obtain < R >
– Run D on input <R>
– If D accepts <R> then run M
2
on input w and do the same thing.
– If D rejects <R> then run M
1
on input w and do the same thing.
• Get contradiction by considering whether or not L(R) ∈ P:
– If L(R) ∈ P, then
• D accepts <R>, since D decides M
P
, so
• L(R) = L(M
2
) by definition of R, so
• L(R) ∉ P.
Application 3: Using Recursion
Theorem to prove Rice’s Theorem
• Rice’s Theorem: Let P be a nontrivial property of Turing-
recognizable languages. Let M
P
= { < M > | L(M) ∈ P }.
Then M
P
is undecidable.
•L(M
1
) ∈ P, L(M
2
) ∉ P.
• D decides M
P
.
• R: On input w:
– Obtain < R >
– Run D on input <R>
– If D accepts <R> then run M
2
on input w and do the same thing.
– If D rejects <R> then run M
1
on input w and do the same thing.
• Get contradiction by considering whether or not L(R) ∈ P:
– If L(R) ∉ P, then
• D rejects <R>, since D decides M
P
, so
• L(R) = L(M
1
) by definition of R, so
• L(R) ∈ P.
• Contradiction!
Applications of Recursion Theorem
• Application 4: Showing non-Turing-recognizability
–DefineMIN
TM
= { < M > | M is a “minimal” TM, that is, no
TM with a shorter encoding recognizes the same
language }.
– Theorem: MIN
TM
is not Turing-recognizable.
– Note: This doesn’t follow from Rice:
• Requires non-T-recognizability, not just undecidability.
• Besides, it’s not a language property.
– Proof:
• Assume for contradiction that MIN
TM
is Turing-recognizable.
• Then it’s enumerable, say by enumerator TM E.
• Define TM R, using the Recursion Theorem:
• R: On input w: …
Application 4: Non-Turing-recognizability
•MIN
TM
= { < M > | M is a “minimal” TM }.
• Theorem: MIN
TM
is not Turing-recognizable.
• Proof:
– Assume that MIN
TM
is Turing-recognizable.
– Then it’s enumerable, say by enumerator TM E.
– R: On input w:
• Obtain <R>.
• Run E, producing list < M
1
>, < M
2
>, … of all minimal TMs, until
you find some < M
i
> with |< M
i
>| strictly greater than |< R >|.
– That is, until you find a TM with a rep bigger than yours.
•Run M
i
(w) and do the same thing.
– Contradiction:
•L(R) = L(M
i
)
• |< R >| less than |< M
i
>|
• Therefore, M
i
is not minimal, and should not be in the list.
Proof of the Recursion Theorem:
Special case

Proof of Recursion Theorem:
Special Case
• Start with easier first step: Produce a TM corresponding
to P
1
:
•P
1
:
–Obtain < P
1
>
– Output < P
1
>
•P
1
outputs its own description.
Q
q(w) = < P
w
>
w
• Lemma: (Sipser Lemma 6.1): There is a
computable function q: Σ* →Σ* such
that, for any string w, q(w) is the
description of a TM P
w
that just prints out
w and halts.
•Proof:Straightforward construction.
Can hard-wire w in the FSC of P
w
.
Proof of RT: Special Case
Q
q(w) = < P
w
>
w
• Lemma: (Sipser Lemma 6.1): There is a
computable function q: Σ* →Σ* such
that, for any string w, q(w) is the
description of a TM P
w
that just prints out
w and halts.
• Now, back to the machine that outputs its own
description…
• Consists of 2 sub-machines, A and B.
• Output of A feeds into B.
• Write as A ° B.
A B

Construction of B
• B expects its input to be the representation <M> of a 1-
input TM (a function-computing TM, not a language
recognizer).
– If not, we don’t care what B does.
• B outputs the encoding of the combination of two
machines, P
<M>
and M.
• The first machine is P
<M>
, which simply outputs <M>.
• The second is the input machine M.
•P
<M>
° M:
B
<M>
< P
<M>
° M >
P
<M>
M
<M>
Some output

Construction of B
• How can B generate < P
<M>
° M >?
– B can generate a description of P
<M>
, that is, <P
<M>
>,
by Lemma 6.1.
– B can generate a description of M, that is, <M>, since it
already has <M> as its input.
– Once B has descriptions of P
<M>
and M, it can combine
them into a single description of the combined machine
P
<M>
° M, that is, < P
<M>
° M >.
B
<M>
< P
<M>
° M >
P
<M>
M
<M>
Some output

Construction of A
•A is P
<B>
, the machine that just outputs <B>,
where B is the complicated machine
constructed above.
• A has no input, just outputs <B>.
A
<B>

Combining the Pieces
•A ° B:
• Claim A ° B outputs its own description, which is < A ° B >.
• Check this…
•A is P
<B>
, so the output from A to B is <B>:
• Substituting B for M in B’s output:
A B
A = P
<B>
B
<B>
A = P
<B>
B
<B>
< P
<B>
° B >

Combining the Pieces
•A ° B:
• Claim A ° B outputs its own description, which is < A ° B >.
• The output of A ° B is, therefore, < P
<B>
° B > = < A ° B >.
• As needed!
•A ° B outputs its own description, < A ° B >.
A B
A = P
<B>
B
<B>
< P
<B>
° B >
Proof of the Recursion Theorem:
General case

Proof of the RT: General case
• So, we have a machine that outputs its own
description.
• A curiosity---this is not the general RT.
• RT says not just that:
– There is a TM that outputs its own description.
• But that:
– There are TMs that can use their own descriptions, in
“arbitrary ways”.
• The “arbitrary ways” are captured by the
machine T in the RT statement.
T
<M>
w
t(<M>, w)

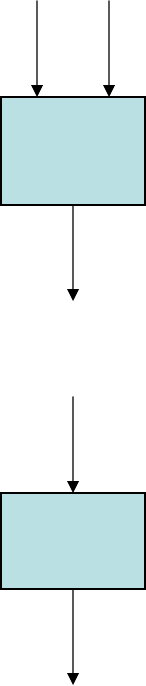
The Recursion Theorem
• Recursion Theorem:
Let T be a TM that computes a
(possibly partial) 2-argument
function t: Σ* ×Σ* →Σ*.
Then there is another TM R that
computes the function r: Σ* →Σ*,
where for any w, r(w) = t(<R>, w).
R
t(<R>, w)
w
T
<M>
w
t(<M>, w)
The Recursion Theorem
• Recursion Theorem:
Let T be a TM that computes a
(possibly partial) 2-argument
function t: Σ* ×Σ* →Σ*.
Then there is another TM R that
computes the function r: Σ* →Σ*,
where for any w, r(w) = t(<R>, w).
R
t(<R>, w)
w
T
<M>
w
t(<M>, w)
• Construct R from:
– The given T, and
– Variants of A and B from the special-
case proof.

Proof of RT: General Case
• R looks like:
• Write this as (A ° B) °
1
T
– The °
1
means that the output from (A ° B)
connects to the first (top) input line of T.
A B
T

Proof of RT: General Case
•R = (A ° B) °
1
T
• New A: P
<B °
1
T>
, where B °
1
T means:
A B
T
B
T

Proof of RT: General Case
•New B:
• Like B in the special case, but now M is a 2-
input TM.
•P
<M>
°
1
M: 1-input TM, which uses output of
P
<M>
as first input of M.
B
<M>
< P
<M>
°
1
M >
P
<M>
M

Combining the Pieces
•R = (A ° B) °
1
T
• Claim R outputs t(<R>, w):
•A is P
<B °
1
T>
, so the output from A to B is <B °
1
T >:
• Now recall definition of B:
•Plug in B °
1
T for M in B’s input, and obtain output for B.
A B
T
w
A = P
<B °
1
T>
B
<B °
1
T >
B
<M>
< P
<M>
°
1
M >
< P
<B °
1
T>
°
1
(B °
1
T) >

Combining the Pieces
• B’s output = < A °1 (B °1 T) > = < R >:
• Now combine with T, plugging in R for M in T’s input:
A = P
<B °
1
T>
B
<B °
1
T > < P
<B °
1
T>
°
1
(B °
1
T) >
A
B
<B °
1
T >
< R>
T
w
A
B
<B °
1
T >
< R>
t(<R>,w)

Combining the Pieces
• Thus, R = (A ° B) °
1
T, on input w, produces
t(<R>,w), as needed for the Recursion Theorem.
T
w
A
B
<B °
1
T >
< R>
t(<R>,w)
R
t(<R>, w)
w
